Can Chaos be utilized as exploration noise for locomotion learning?
Worasuchad Haomachai and Poramate Manoonpong
Nanjing University of Aeronautics and Astronautics, Nanjing, China
Vidyasirimedhi Institute of Science & Technology, Rayong, Thailand
Introduction
There is compelling evidence to support that chaotic patterns of behavior exist in many biological systems. For example, Maye et al. observed behavioral indeterminacy (comparable to a chaotic pattern) during spontaneous flight maneuvers (searching behavior without any external cues) in Drosophila fruit flies. This suggests that chaotic dynamics may be involved in the biological neural control underlying spontaneous behavior. It also raises the question, “Can chaos be utilized in artificial neural control for robot locomotion learning?” To address the question, this study investigates and compares the use of chaotic exploration noise and standard Gaussian noise for robot locomotion learning. Although chaos has been used to tackle machine learning problems (such as classification), until now, it is yet to be thoroughly explored for locomotion learning.
Material and Methods
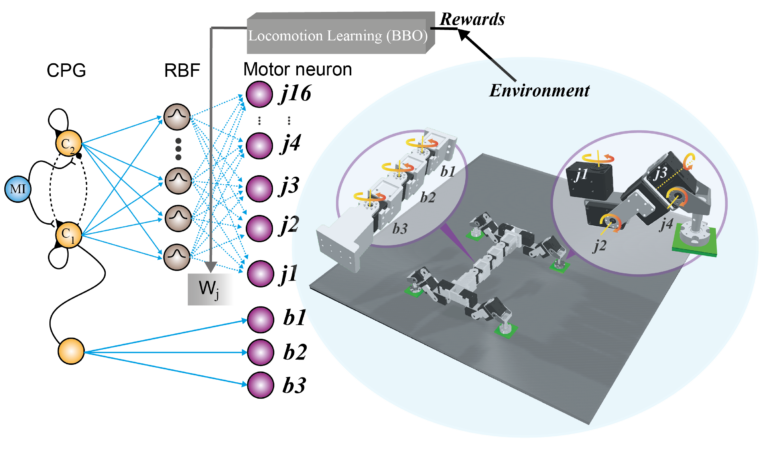
- We construct a locomotion controller as a reinforcement learning framework, so that our robot (here, a gecko-like robot) has to learn to walk. The controller, configured as a neural central pattern generator (CPG) with a radial basis function (RBF)-based premotor neuron network.
- The robot joint trajectories are encoded in the output weights connecting the CPG-RBF network to the motor neurons (dashed lines in Fig). The output weights are learned using a probability-based black-box optimization (BBO) approach to optimize joint trajectories with respect to robot walking performance.
Experiment and Results
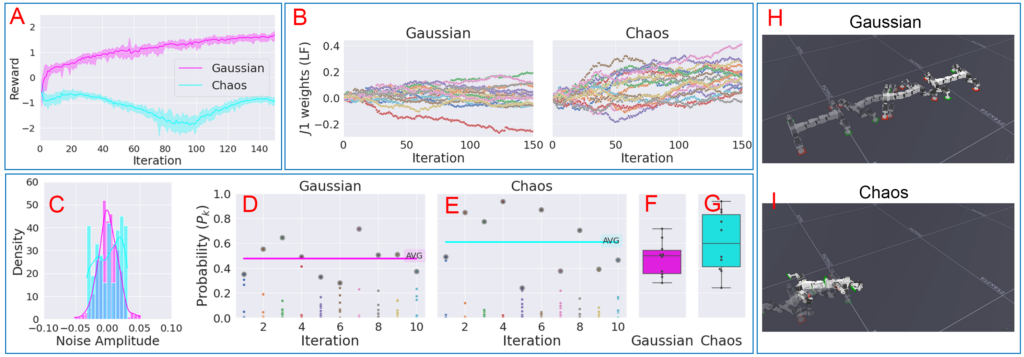
- We aim to determine whether chaotic noise can be utilized as a perturbation noise to optimize control parameters (output weights) in BBO. Thus, we let the robot learn with chaotic noise and compared its locomotion learning performance to Gaussian noise.
- Due to the asymmetric profile and chaotic dynamics (Fig.C), the control parameters might change quickly at the beginning, subsequently converting to a certain parameter space, as observed in the weight changes of j1 of LF (Fig.B). Based on the analysis of BBO during the first ten iterations, we observed that the highest probability 𝑃_𝑘 of chaotic noise tends to fluctuate and dominate by performing undesirable behaviors (Fig.E). The average value of the highest 𝑃_𝑘 in each iteration was 0.60 with an SD of 0.27 (Fig.G). Undesirable behaviors that dominate at the beginning can quickly lead the optimization process in the wrong direction. As a consequence, the optimization process could get stuck at the local optima, preventing the robot from forming a stable gait for walking forward (Fig.I).
- The symmetric profile of Gaussian noise can slowly adapt the parameters, leading to a balance of positive and negative parameter values with lower probability and a variant of 𝑃_𝑘 (Fig.D and F). The average of the highest 𝑃_𝑘 in each iteration was 0.47 with an SD of 0.13 (Fig.F). This results in preventing divergence (Fig.B) where a stable gait can be formed (Fig.H).
Conclusion & Future work
- Our investigation reveals that chaos cannot be directly utilized as exploration noise in BBO for locomotion learning.
- Although chaotic noise fails for locomotion learning here, it seems to facilitate learning speed (i.e., it can adapt parameters faster than Gaussian noise). Therefore, we will further explore an alternative strategy that uses chaotic dynamics to accelerate the overall optimization process of BBO with Gaussian noise for fast and stable locomotion learning.
Citation
@INPROCEEDINGS{haomachaiamam2023,
author={Haomachai, Worasuchad and Manoonpong, Poramate},
booktitle={The 11th International Symposium on Adaptive Motion of Animals and Machines (AMAM2023). 2023, p. 53-54},
title={Can Chaos be utilized as exploration noise for locomotion learning?},
url={https://doi.org/10.18910/92263}
}Acknowledgements
This work was supported by the National Key R&D Program of China. We thank the CM labs for providing Vortex.